Digital Logic 101

I am going to start by assuming you’ve seen truth tables for different logical operations. For example, you might have seen the input output mapping for an ERASE1, or “erase to \(1\)”, gate: if the input is \(1\), it stays \(1\); if the input is \(0\), it becomes \(1\). This describes the logic of the gate, but it doesn’t describe the physics. Physically, a \(0\) and a \(1\) correspond to two different configurational states of some physical degrees of freedom: two different possible responses a physical substrate can have based on some forces applied to the system. This configurational state could be the velocities and positions of the free electrons in a material (as is the case for CMOS circuits) or the Josephson phase difference across a Josephson Junction (as is often the case in superconducting logic), but this information can ultimately be stored in any physical degree of freedom. Even something as simple as the phase space position of a single particle in one dimension can serve as a viable candidate for information storage. In this context, you might choose \((x,v)=(-1,0)=\Gamma_0\) and \((x,v)=(+1,0)=\Gamma_1\) as your configurational states corresponding to \(0\) and \(1\), respsectively.

An important property of good information storing states is that they must be stable. We want a \(0\) to stay a \(0\) until we say otherwise. So, you can see why we have chosen both states to be characterized by zero velocity. Of course, in any real physical setting there is inherent noise and uncertainty. The probability of being at an exact point in phase space \(\Gamma_i\) is vanishingly small, so it makes more sense to define the \(0\) as some region around \(\Gamma_0\). For example, even if we could assure that the particle is exactly at \(\Gamma_0\) or \(\Gamma_1\) at \(t=0\) (first image blelow), this knowledge degrades over time due to diffusion. The sketches below show this process; the shaded region represents the probability density of the particle, and we see it growing as time progresses from left to right. In the abscence of any other external forces, the most likely position will remain fixed, but the range of positions that the particle also might be grows as \(\sqrt{t}\). So, our memory state at time \(t\) is really some distribution \(\rho_0(\rho_1)\) over configurations centered on some phase space point \(\Gamma_0(\Gamma_1)\), with a variance that depends on a balance of noise and control in the system.

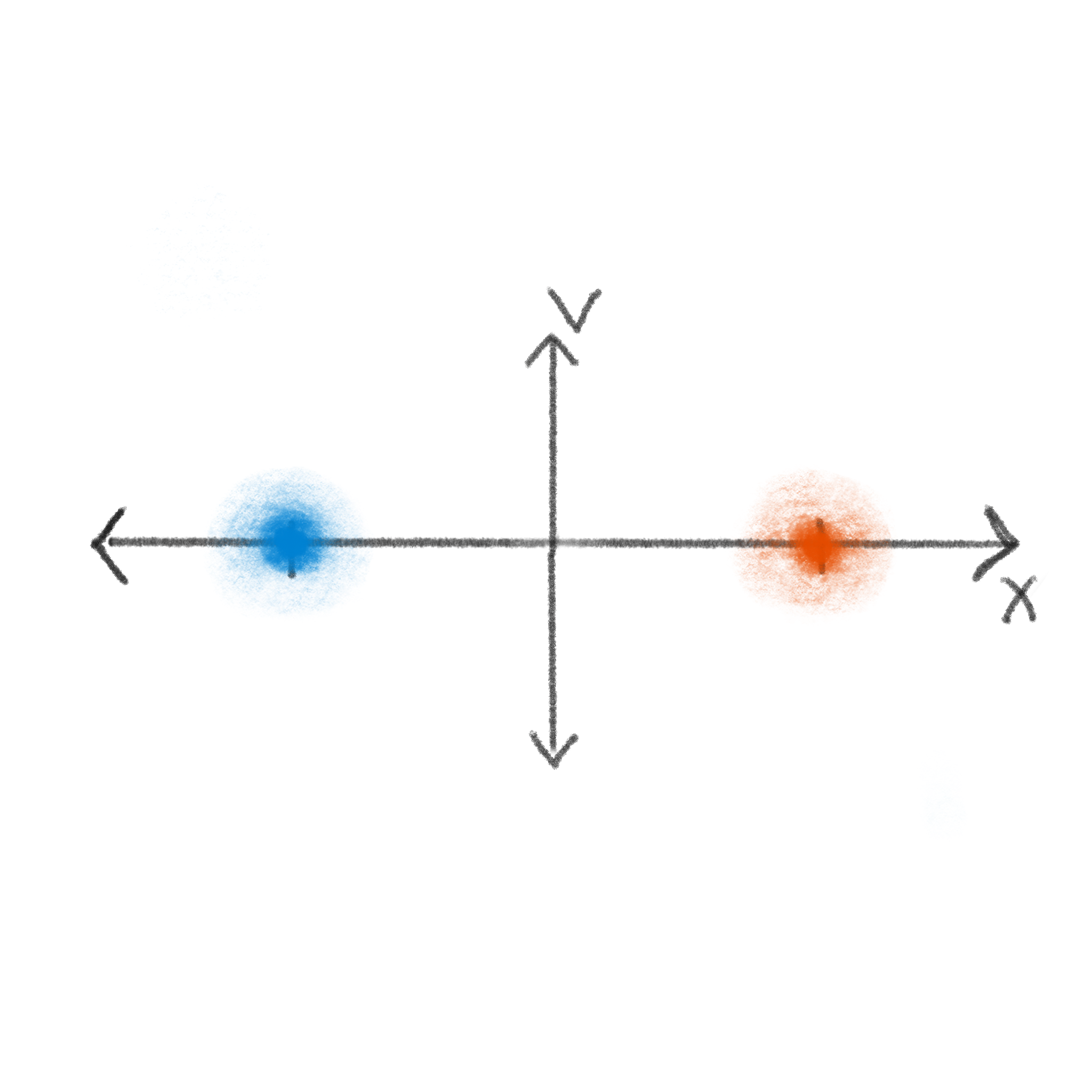
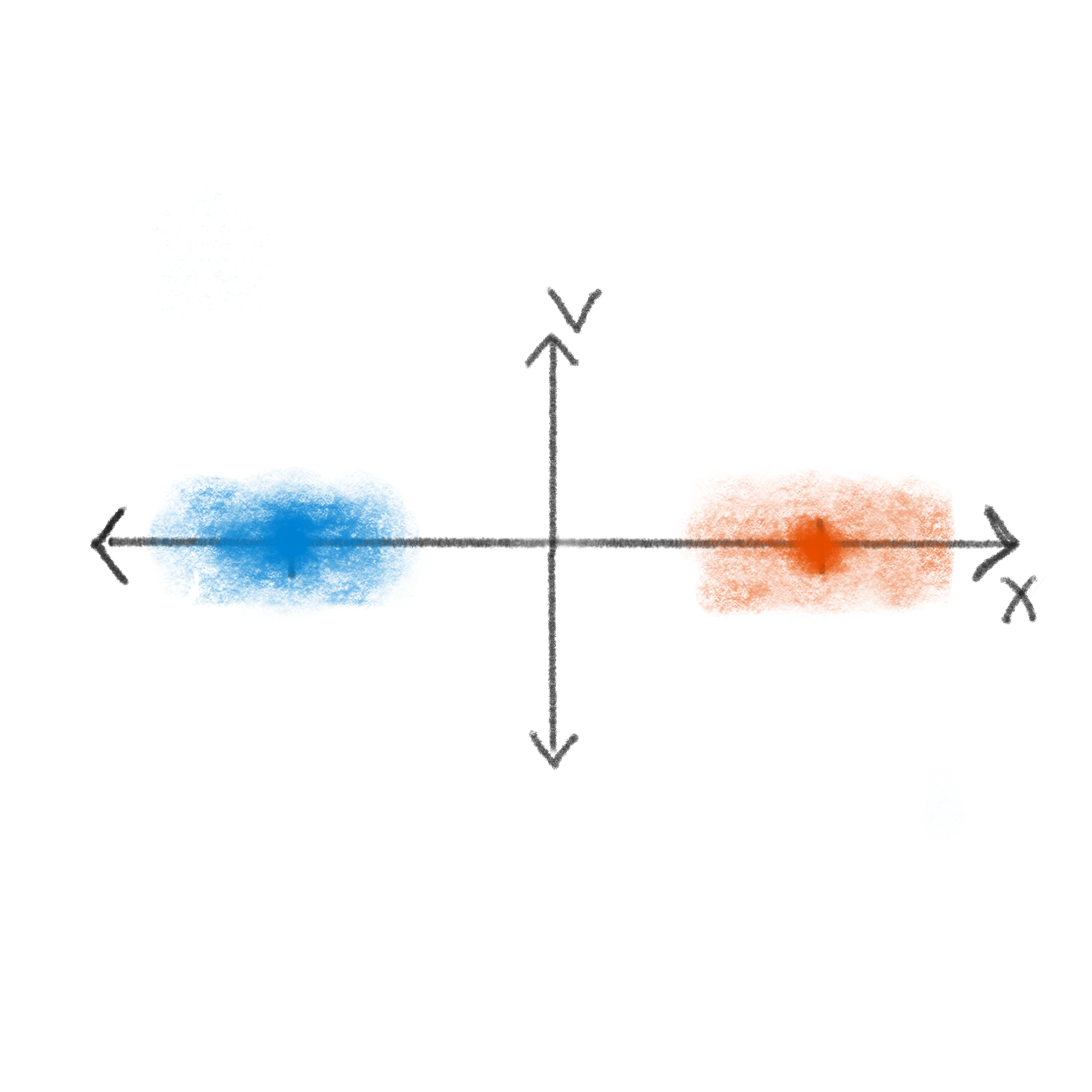
at t=0 the distribution is very narrow by t=1, the velocity distribution has reached the boltzman distribution, but the position variance continues to grow by t=4, the position variance has doubled

This brings us to the second important property when choosing good information storing states: they must be distinguishable. We need to make sure that the variance of the distribution is much smaller than the distance between the informational states. The narrower this distribution is relative to the length scale of the information storage, the more precise we can compute. Looking at the figures above, you can see that the velocity distribution saturates at some point (after reaching the Maxwell-Boltzman distribution), given a fixed environment. The position distribution however, continues to grow. Given this, it is common to choose the memory state position centers to be located at stable energy minima according to some drive on the system. Being near the minima combats the inherent diffusive forces of the environment, halting the growth of the distribution at something like the second image above. For example, if we represent the drive with a potential energy surface, our \(0\) and \(1\) distributions may look like this:

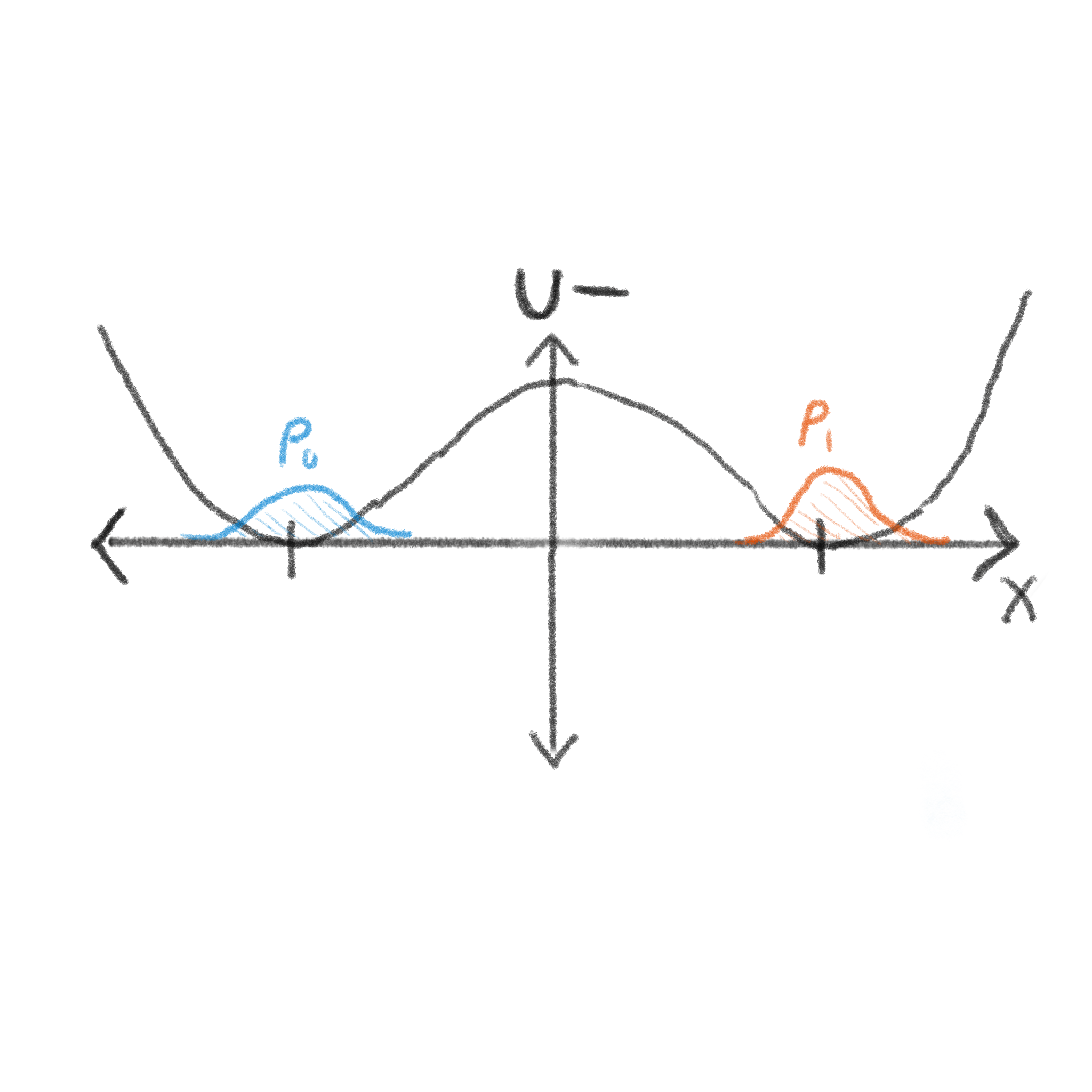
position space distribution

From this perspective, the operation of the ERASE1 gate is straightforward:

  1. We first initialize our particle with an input state. This means some kind of intervention that sets its position and velocity to be consistent with sampling from our initial ditribution for \(0\) or \(1\). A common way to do this is to setting the external drive (forces) such that both the \(0\) and \(1\) distributions are time invariant attractors, like the potential energy surface above. Whichever the particle starts closest to will likely be the resulting input logical state.
  2. Next, we exert forces on the particle over time such that particles around the phase space point \(\Gamma_0\) end up at \(\Gamma_1\) while those near \(\Gamma_1\) remain unaffected. Importantly, this second part must be done without peeking at which logical state you start in (if you allow peeking, you introduce a “Maxwell’s demon” into the system which basically kicks the can down the road in terms of physics and information processing).
  3. If this information needs to be stored, we want to end by returning to the drive for which the distributions corresponding to \(0\) and \(1\) are invariant.

We can sketch this out with a very simple cartoon to depict each step:
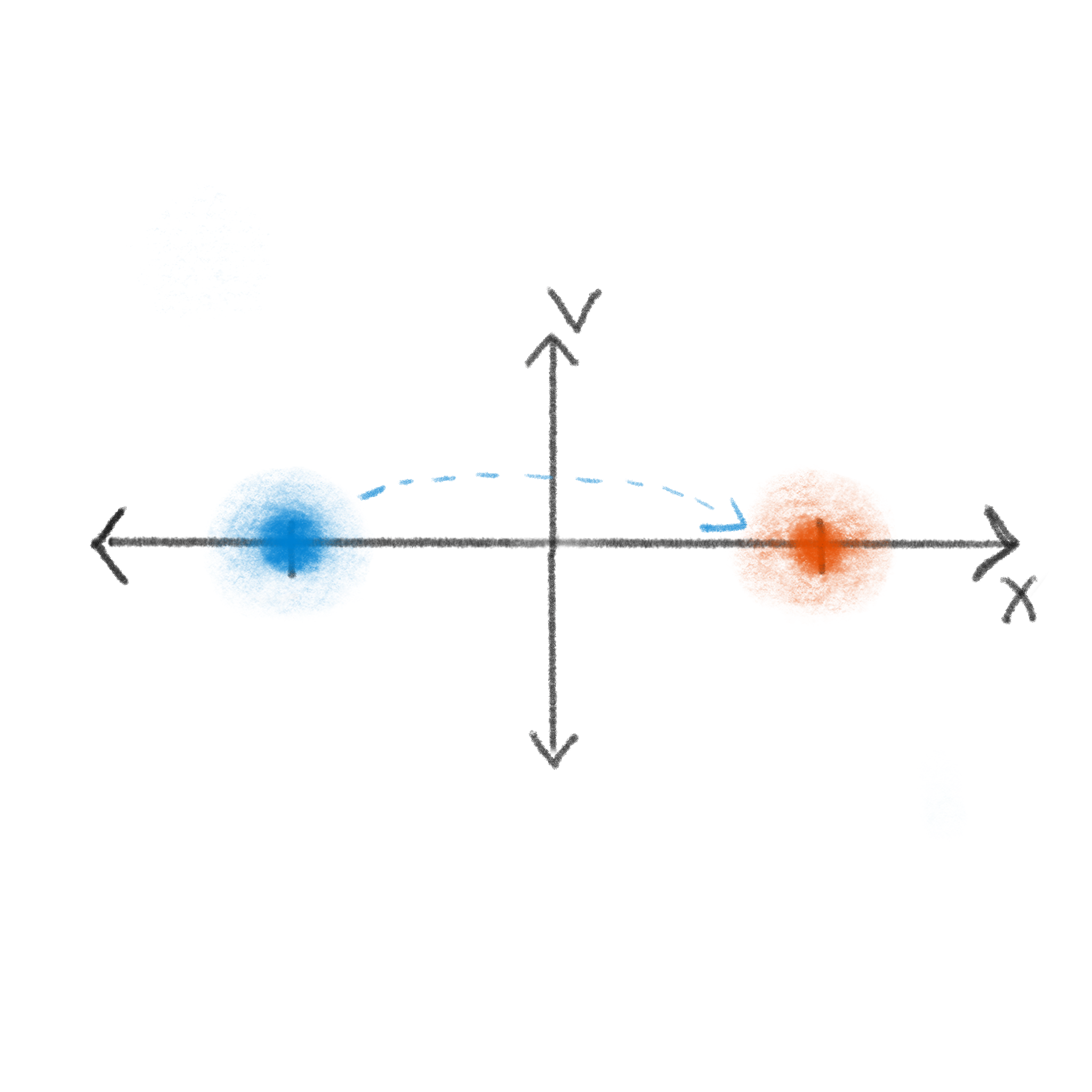
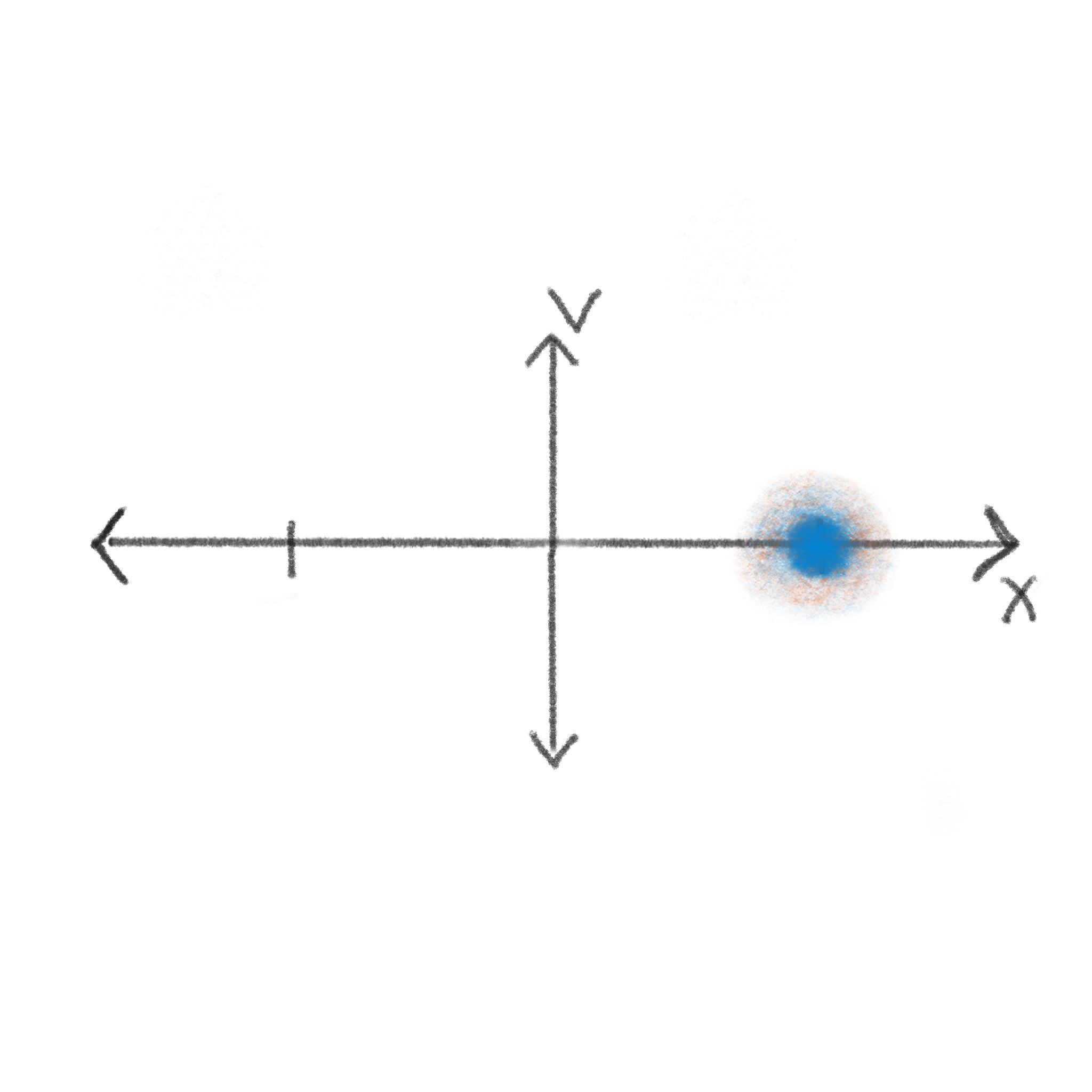
step 1 step 2 step 3

Ok, thanks… but aren’t we supposed to be talking about Reversibility?

Right! Ok. There are three distinct meanings of “reversible” that are often used within a single conversation. I want to talk about each, but first we need to talk about energy. Computing costs energy. The ERASE1 gate discussed above has a minimal energetic cost associated with it, no matter what the implementation is. This cost is due to Liouville’s Theorem, which dictates a preservation of global phase space density and Thermodynamics, which describes the behavior of the system’s thermal environment. In short: Liouville’s says the compression of two distinct start states into a single end state is not possible without a corresponding expansion in the environment; Thermodynamics says such an expansion in an environment of temperature \(T\) implies the operation must cost, on average, at least \(k_B T \ln 2 \approx .7 k_B T\) Joules of energy. Because this logic gate requires state space compression, it is considered an “irreversible” logic gate. Conventional CMOS logic is based off of such irreversible operations, so we often think of this energy scale as the theoretical energy scale of efficient computing (I call this unit the “Landauer”, after Rolf Landauer who first explained the bound.)

Logical Reversibility

The property of the ERASE1 gate that gives it this lower bound on work cost is known as “logical irreversibility”. You can build a universal computer using only logically irreversible gates, but you can also do it out of “reversible” ones (or, realistically, a combination of the two). It’s easy to tell from a truth table whether a gate is logically reversible or not: if you cannot reconstruct the input from the output, it is logically irreversible; if you can reconstruct the input, it is logically reversible. In the case of the ERASE1, the output is a \(1\) no matter what– so you will not be able to tell what the input was just by reading the output. Reversible gates (a NOT gate, for example) allow you to reconstruct the input, which is indicative of there being no state space compression; consequently reversible logic gates (NOT, CNOT, FREDKIN, etc…) do not have this lower theoretical bound on cost.

That being said, conventional computers in no way operate near the energy scale of these bounds. All consumer computers operate at least 4, more likely 5, orders of magnitude above this efficient energy scale. So the energetic difference between logically reversible and irreversible gates, which is on the order of 1 Landauer is not a particularly meaningful engineering constraint for CMOS devices at the moment. If you can build a computer from only irreversible gates that operates at a few Landauers per operation you have revolutionized computing costs by several orders of magnitude. A computer made from only reversible gates than operates at .2 or .3 Landauers per operation might save you another order of magnitude, but it’s basically the same kind of revolution. Those two systems are much closer to eachother in efficiency than to the status quo. A logically reversible gate would need to operate at a small fraction of a Landauer (.001, for example) in order to be a revolution over an optimized irreversible gate. And, while a logically reversible gate is theoretically capable of achieving this kind of efficiency, that is only relevant if someone has a workable substrate and design that can realistically achieve it. That is an important if, because what dictates the actual cost of a logic gate in practice is not the logical reversibility of the gate, but the thermodynamic reversibility of the physical process that underlies the gate’s implementation.

Thermodynamic Reversibility

Thermodynamic reversibility is a completely different concept than logical reversibility. Both logically reversible and irreversible gates can be instantiated using protocols that are both thermodynamically reversible and irreversible. Thermodynamic reversibility characterizes how much of the work done in the process is irretrievable. The ERASE1 gate’s minimal work cost is retrievable at a later time because during the erasure 1 Landauer of energy is stored in the nonequilibrium free energy of the joint particle/control apparatus system. It’s like compressing a spring. Compressing a spring requires energy, but you can get that energy back when you allow the spring to relax. However, any extra work you did while compressing the spring that goes beyond its storage capacity will be forever irretrievable. In this analogy, a thermodynamically reversible compression uses the exact amount of energy the spring is capable of storing, and no more.

In order to be truly thermodynamically reversible, a system must stay in local equilibrium with its environment at all times. In practice this means quasi-static or adiabatic protocols. This kind of protocol is very slow on the timescale that the system’s high probability regions relax to the local thermal distribution, meaning that even as you change the forces over time the system has plenty of time respond and equilibrate to the new drive before it is changed again. This assures that all the work you are doing is stored in the nonequilibrium free energy and so will be retrievable. Because the distribution is locally equilibrated, the velocity distribution is always centered at \(v=0\) with a variance that depends on the temperature– this restricts thermodynamically reversible processes to a narrow swath of phase space, like this:

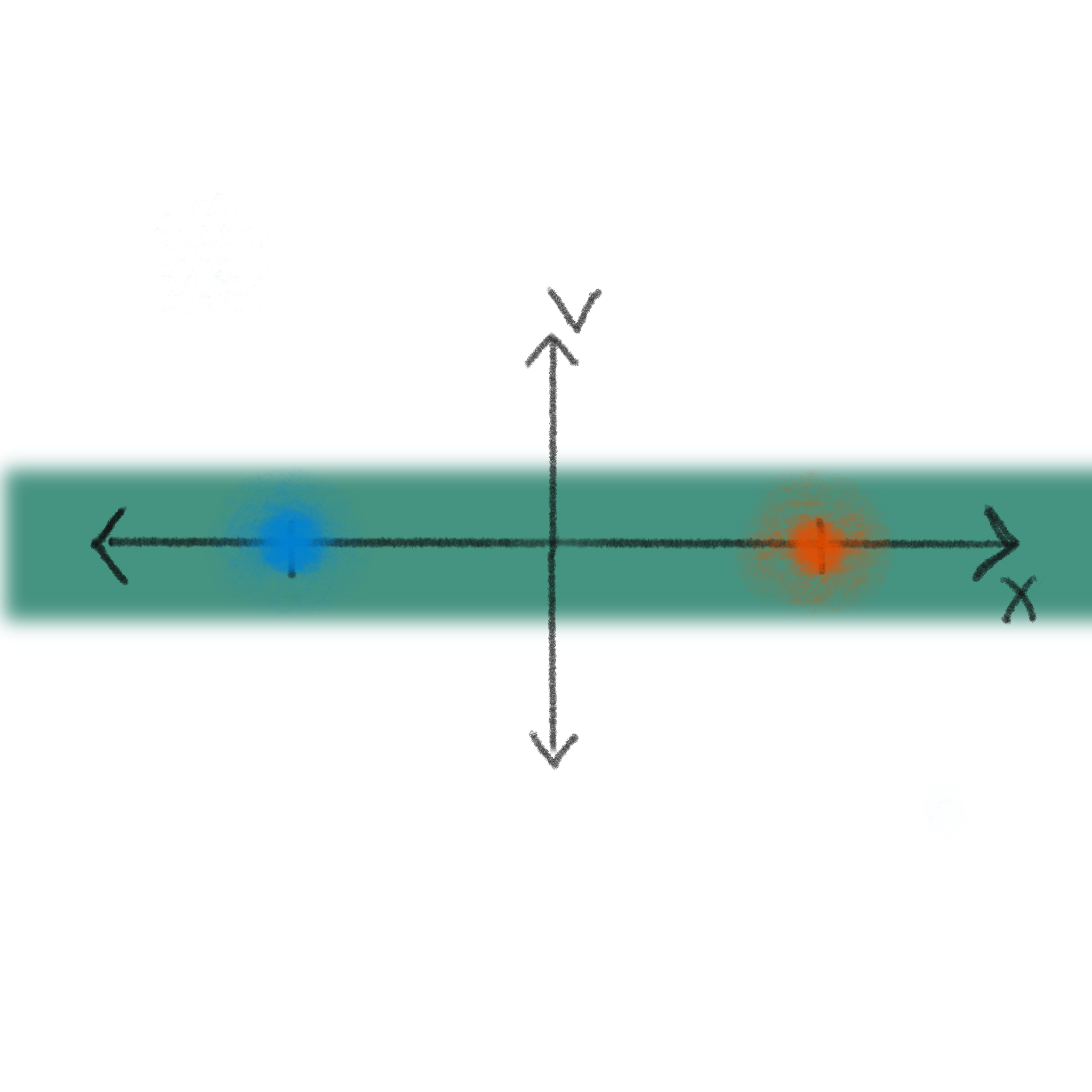
step 3

Reversible Computers

A third concept of reversibility is the idea of reversibility of a computer. Here, the “reversible” refers to the entire computer’s configuration, and ensuring that the computers final state post-computation matches its initial state pre-computation. The original idea of a reversible computer goes back to the 60’s. The basic idea is that you compute without ever throwing away information (using ony logically reversible logic gates). Once your result is read out (this costs some energy proportional only to the size of the output and not the difficulty of the computation), you then reverse all of the computations: returning to the initial state and ready for another computation. If each reversible logic gate is implemented in a thermodynamically reversible way, all the intermediate steps cost no work (since logically reversible gates have no lower bound on necesarry work). Thus you have a very low power computer, that scales with input/output size regardless of the computation.

Surprisingly, this same idea can be implemented using logically irreversible gates as well. Assume that the inital state of each bit in the computer is random with a 50/50 bias. You then start by inputting the problem (setting some small percentage of them to a known value), and use irreversible logic to come to an answer accessing each gate only one time. This will cost at least a Landauer per ERASE operation (it can only reach this bound if the process is thermodynamically reversible). However, once the output is read out– we must return to the computer’s initial state. This is accomplished by re-randomizing each gate that was triggered in the computation (this is known as bit creation, the oppposite of erasure). At peak efficiency, creation serves as “relaxing the spring” and allow us to recapture 1 Landauer for each bit randomized. Thus, the net work cost will again depend only on the input/output process and not the complexity of the computation.

These kind of computers are certainly theoretically possible, but various attempts and designs have yet to prove both practical and engineerable. The number of gates necessary is larger, and the timing architecture is more complicated than the current CMOS systems. Additionally, thermodynamically reversible protocols leverage a heavy penalty on the speed of computations (thermodynamically reversible means very slow compared to local thermalization, so there is a speed limit set by the thermalization time.) This problem plagues efficient non-reversible computer designs too, but because each gate must be “uncomputed” in the reversible computer, we pay the cost of the inefficiency twice. This kind of design depends heavily on the establishment of scalable gates that can operate near the fundamental thermodynamic bound, so the design of such gates is a more pressing matter.

ASIDE: How does Momentum Computing Fit Into all of this?

Momentum Computing is a design methodology for protocols. It is, then, rather removed form concepts about computers that are reversible in the sense of having a cost that scales only with the size of the input/output processes. It is also removed the the idea of logical reversibility, since it can be used to design logically irreversible and logically reversible gates. Rather, it is a way to design implementations of logic gates that circumvent the issue of the adiabatic speed limit. Think of it as an alternative to the standard perspective on thermodynamic reversibility. A physically realizeable version of a momentum computing protocol is not thermodynamically reversible, it satisfies itself with being simply thermodynamically cheap. Recall the three steps of the computation:

  1. We first initialize our particle by sampling from either the \(0\) or \(1\) distribution.
  2. Next, we exert forces on the particle over time such that particles around each memory state center \(\Gamma_{in}\) end up near their intended \(\Gamma_{out}\) (no peeking).
  3. We end by making sure the output state is sampled from either \(0\) or \(1\).

Momentum Computing recognizes that there is a lot of flexibility in step two. Rather than assuming that the velocity distribution is constantly relaxing to zero mean during the protocol, we assume that the system is in the underdamped regime and dominated by the dynamics of the driving force instead of the statics. This allows us to drive the particle far out of equilibrium at great work cost, but then recapture the majority of that energy at the end because we operate faster than the environment dissipates that energy into the environment. This opens up the entire phase space to play with, instead of just the swath nearest to \(v=0\). As such, we can impart different velocities to different initial states– distinguishing them by their velocity distributions rather than just the distribution over position. The win here is that we can access low cost computation, but in a significantly shorter amount of time (there may also be a win in terms of the energetic price of logical fidelity, but that is a different topic.)

In any realistic setting the damping wont be exactly zero and our control won’t be exactly perfect. The result is that step 3 becomes quite important when compared to adiabatic protocols. In the adiabatic case, the final distribution is by definition a locally thermalized distribution conjugate to whatever the driving forces are doing at the time. So, with the correct final drive, you already know the output state is properly sampled from the target distributions.

For momentum computing, a careful intervention must be made in step 3 so that the distribution is as close to our target distributions as possible. Step 3 is where you pay the cost of diffusion and dispersion of the initial distribution that occurs due to the dynamics of the information processing. The adiabatic protocol avoids these costs through constant thermalization. A simple way to accomplish this, assuming the thermal coupling can be tuned, is to set the damping to be large right at the begininng of step 3 which will cause the system to relax very quickly. The damping can then be set low again during the next computation. In the absence of tunable damping other interventions might be possible to accelerate the transition to the target distribution.

Here is a brief list of what has been demonstrated with momentum computing thus far:

  • Physically artificial simulations that show perfect fidelty and zero work cost in the limit of zero damping when performing logically reversible computations (logically irreversible computations, of course, cannot be accomplished with zero work cost nor can they be accomplished with zero damping). At increased dampings, the fidelity and work have been shown to decrease and increase, respectively, but the transition is smooth.
  • Physically realistic (nonzero damping, restricted control, fabrication viable parameters) circuit design and simulations that can perform a NOT gate at a cost of .4 Landauers in a matter of a few nanoseconds.
  • Physically artificial simulations that show momentum based protocols can perform ERASE gates at a cost of about 2 Landauers
  • Anomalous non-monotonic work costs and fidelity, that differ qualitatively from adiabatic and counterdiabatic protocol results.