The Thermodynamic Uncertainty Theorem
New Paper!
Hi there, this is just a quick update to post about my newest publication in PRE, The Thermodynamic Uncertainty Theorem. You can check out the full paper through that link, but I’ll also post the abstract below:
- Thermodynamic uncertainty relations (TURs) express a fundamental lower bound on the precision (inverse scaled variance) of any thermodynamic charge — e.g., work or heat—by functionals of the average entropy production. Relying on purely variational arguments, we significantly extend TUR inequalities by incorporating and analyzing the impact of higher statistical cumulants of the entropy production itself within the general framework of time-symmetrically-controlled computation. We derive an exact expression for the charge that achieves the minimum scaled variance, for which the TUR bound tightens to an equality that we name the thermodynamic uncertainty theorem (TUT). Importantly, both the minimum scaled variance charge and the TUT are functionals of the stochastic entropy production, thus retaining the impact of its higher moments. In particular, our results show that, beyond the average, the entropy production distribution’s higher moments have a significant effect on any charge’s precision. This is made explicit via a thorough numerical analysis of “swap” and “reset” computations that quantitatively compares the TUT against previous generalized TURs.
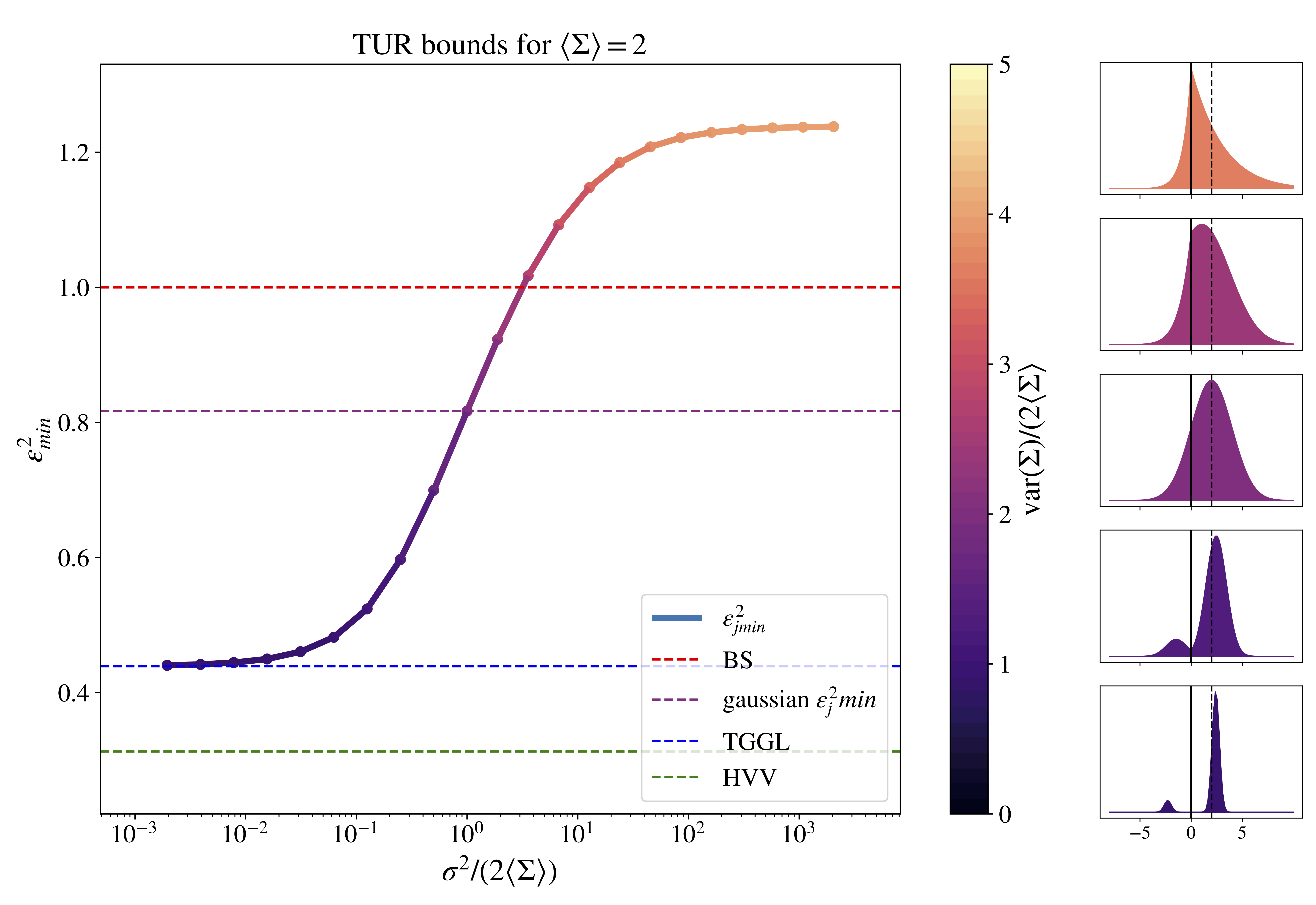
So… what does all that mean? What’s going on in that picture?
This is what the figure depicts: the minimal noise-to-signal ratio for a family of distributions that keeps the average fixed while varying the variance.
The article comes within the context of a slew of results over the last 5 or so years on a family of inequalities called ‘thermodynamic uncertainty relations’ (TURs). To be very general: these relations set a bound on the accuracy of observables in the system based on how much energy the system is dissipating into the environment on average.
What we show is that the accuracy of the observables is determined by more than just the average dissipation in the system. We come up with a relation that tells us the most accurate observable possible based on all moments (mean, variance, skewness, kurtosis, etc…) of the dissipation. From this perspective, we can keep the average dissipation constant (this causes the previous TURs to look like straight lines) and see how changing even just the variance of the dissipation distribution has pretty interesting effects on the most accurate current possible.